Bubble sort is a simple sorting algorithm, which compares repeatedly each pair of adjacent items and swaps them if they are in the incorrect order. At the first run, the highest element of the list ends on the last place of the sorted list, and then, at the following run, the next highest element ends on one position lower than the previous element and so on. The initial list is finally sorted, when at a run, no swaps occur.
Even though it’s one of the simplest sorting algorithms, it’s almost never used in real life because of the bad performance on large sorting lists. It’s easy to learn, so it’s one of the first algorithms that people learn.
Step by step example :
Having the following list, let’s try to use bubble sort to arrange the numbers from lowest to greatest:
Unsorted list: 9 2 0 1 4 6
First run:
(9 2 0 1 4 6) -> (2 9 0 1 4 6) : 9>2, swap occurs
(2 9 0 1 4 6) -> (2 0 9 1 4 6) : 9>0, swap occurs
(2 0 9 1 4 6) -> (2 0 1 9 4 6) : 9>1, swap occurs
(2 0 1 9 4 6)-> (2 0 1 4 9 6) : 9>4, swap occurs
(2 0 1 4 9 6) -> (2 0 1 4 6 9) : 9>6, swap occurs. The last two elements are in the right order, no swaps occur, it’s the end of the first run.
Second run:
(2 0 1 4 6 9) -> (0 2 1 4 6 9) : 2>0, swap occurs
(0 2 1 4 6 9) -> (0 1 2 4 6 9): 2>1, swap occurs
(0 1 2 4 6 9) -> (0 1 2 4 6 9): 2<4, no swap occurs
(0 1 2 4 6 9) -> (0 1 2 4 6 9): 4<6, no swap occurs
(0 1 2 4 6 9) -> (0 1 2 4 6 9): 6<9, no swap occurs, it is the end of the list -> end of the second run.
The array is already sorted, but the algorithm doesn’t know that, so it requires another pass with no swaps in order to know the elements are in the right place.
Third run:
(0 1 2 4 6 9) -> (0 1 2 4 6 9): 0<1, no swap occurs
(0 1 2 4 6 9) -> (0 1 2 4 6 9): 1<2, no swap occurs
(0 1 2 4 6 9) -> (0 1 2 4 6 9): 2<4, no swap occurs
(0 1 2 4 6 9) -> (0 1 2 4 6 9): 4<6, no swap occurs
(0 1 2 4 6 9) -> (0 1 2 4 6 9): 6<9, no swap occurs
The algorithm now knows that the list is sorted.
Sample code:
#include < iostream >using namespace std;
int main()
{int a[100]; // The sorting array
int n; // The number of elements
cout << "Please insert the number of elements to be sorted: ";
cin >> n; // The total number of elements
for(int i=0;i< n;i++)
{cout << "Input " << i << " element: ";
cin >>a[i]; // Adding the elements to the array
}cout << "Unsorted list:" << endl; // Displaying the unsorted array
for(int i=0;i< n;i++)
{cout << a[i] << " ";
}int flag=-1; // The flag is necessary to verify is the array is sorted, 0 represents sorted array
int k=n; // Another variable is required to hold the total number of elements
while(flag!=0 && k>=0) // Conditions to check if the array is already sorted
{k=k-1;
flag=0;
for (int i=0;i < k;i++)
{if(a[i]>a[i+1]) // Check if the two adjacent values are in the proper order, if not, swap them
{int aux=a[i]; // The swap procedure
a[i]=a[i+1];
a[i+1]=aux;
flag=1; // A swap has taken place, this means a new run of the algorithm must take place
} // to determine if the array is sorted.
}}cout << "nSorted list:" << endl; // Display the sorted array
for(int i=0;i < n;i++)
{cout << a[i] << " ";
}return 0;
}
Output:
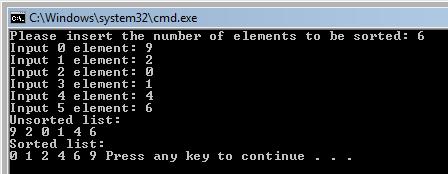
Code explanation:
while(flag!=0 && k>=0)
{k=k-1;
flag=0;
...
}
A flag is required to check if any swaps have occurred at a run of the algorithm. If a swap has taken place, the flag becomes 1, and the while loop gets at least one more pass. When the flag is 0, it means that no swap has taken place so the arrays has been sorted and the while loop gets ignored.
Also, the k must be greater or equal to 0, this represents the number of elements of the list, and at each pass it decrements its value by 1. If this condition and the previous one are both true at the same time, then the array isn’t sorted, and the program enters the while loop. If one of the conditions is false, then the array has been sorted out.
Complexity:
Compares – there is a for loop embedded inside a while loop (n-1)+(n-2)+(n-3)+ … +1 which results in O(n^2), Swaps – Best Case 0, or O(1) and on Worst Case (n-1)+(n-2)+(n-3) + … +1 , or O(n^2).
Advantages:
- it is easy to learn;
- few lines of code;
- works very well on already sorted lists, or lists with just a few permutations.
Disadvantages:
- not effective for large numbers of sorting elements;
- complexity is O(n^2).
Conclusion:
It is the best algorithm to begin learning sorting algorithms because it is the simplest. It is very easy to implement in every programming language. In computer graphics it is popular for its capability to detect a very small error (like swap of just two elements) in almost-sorted arrays and fix it with just linear complexity (2n). Also, the bubble sort is considered a comparison algorithm, as it compares the elements at each run.

