C Algorithms – Dijkstra’s Algorithm – IT Training and Consulting

This algorithm is a graph search algorithm that solves the shortest path problem for a graph.

In the graph, the path between vertices has a cost or a length, so Dijkstra’s algorithm simply determines the path with the lowest cost between a vertex and another. The algorithm ends when the shortest path from a vertex to a destination vertex was discovered.

How it works:

1) First thing to do is to set the distance value, which is 0 for the current node and infinity for the rest.
2) Set all the nodes as unvisited and initial node as current one;
3) For the current node, calculate the possible distances to the neighbors (if A has distance of 1 and a connecting node B has distance of 4, then the distance from A to B will be 1 + 4 = 5) If this distance is less than the previous recorded one, overwrite it with the newer one. Also, you have to add the unvisited neighbors to the unvisited list;
4) After we have finished checking all the connecting nodes, mark the node as visited. The distance that was recorded is final and minimal;
5) The next current node will be the node with the lowest distance in the unvisited set.
6) If all nodes have been visited, finish. Otherwise, set the unvisited node with the smallest distance (from the initial node, considering all nodes in graph) as the next "current node" and continue from step 3.

Step by step example:

Let us take a peek at a simple example, here is the graph:

As you can see, A is the starting node, the distance to B is 1 and the distance to C is 5, so we co to B:

If you look closely when we were in A, the distance to D was infinite, because at that time we had no path to D from A, but since we are in B, we have a new distance. Also, the best distance to choose now is D because it is the shortest:

And finally, we are left with only one option, the route is direct through E:

Now we have to identify the route. The previous node of E is D, and the previous node of D is B, and B’s previous node is A. So the best route is ABDE. In this case, the total weigh is 4 (1+2+1).

Sample code:

```
 #include<iostream>
```
```
 #include<stdio.h>
```
```
using namespace std;
```
```
int shortest(int ,int);
```

int cost[10][10],dist[20],i,j,n,k,m,S[20],v,totcost,path[20],p;

```
 
```
```
int shortest(int v,int n)
```
```
{
```
```
	int min;
```
```
	for(i=1;i<=n;i++)
```
```
	{
```
```
		S[i]=0;
```
```
		dist[i]=cost[v][i];
```
```
	}
```
```
	path[++p]=v;
```
```
	S[v]=1;
```
```
	dist[v]=0;
```
```
	for(i=2;i<=n-1;i++)
```
```
	{
```
```
		k=-1;
```
```
		min=31999;
```
```
		for(j=1;j<=n;j++)
```
```
		{
```
```
			if(dist[j]<min && S[j]!=1)
```
```
			{
```
```
				min=dist[j];
```
```
				k=j;
```
```
			} 
```
```
		}
```
```
		if(cost[v][k]<=dist[k])
```
```
			p=1;
```
```
		path[++p]=k;
```
```
		for(j=1;j<=p;j++)
```
```
			cout<<path[j];
```
```
		cout <<"n";
```
```
		//cout <<k;
```
```
		S[k]=1;
```
```
		for(j=1;j<=n;j++)
```

			if(cost[k][j]!=31999 && dist[j]>=dist[k]+cost[k][j] && S[j]!=1)

```
				dist[j]=dist[k]+cost[k][j];
```
```
	}
```
```
	return v;
```
```
}
```
```
 
```
```
int main()
```
```
{
```
```
	int c;
```
```
	cout << "Enter number of vertices = ";
```
```
	cin >> n;
```
```
	cout << "Enter number of edges = "; 
```
```
	cin >>m;
```
```
	cout <<"nEnternEDGE Costn";
```
```
 
```
```
	for(k=1;k<=m;k++)
```
```
	{
```
```
		cin >> i >> j >>c;
```
```
		cost[i][j]=c;
```
```
	}
```
```
 
```
```
	for(i=1;i<=n;i++)
```
```
		for(j=1;j<=n;j++)
```
```
			if(cost[i][j]==0)
```
```
				cost[i][j]=31999;
```
```
	cout <<"enter initial vertex";
```
```
	cin >>v;
```
```
	cout << v<<"n";
```
```
	shortest(v,n);
```
```
	return 0;
```
```
}
```

Output:

Code explanation:

Just like in the example that I explained earlier, at first it sets the distance of 0 for the current node, next the path to the connecting nodes is checked. The minimal distance will be retained in the min variable, of course after it is checked to be the absolute minimal distance at that point. Also, the cost is compare to the previous value that may exist, and if it is smaller, it will replace the old value. This procedure repeats until there are no more nodes to check.

A visual representation of the graph:

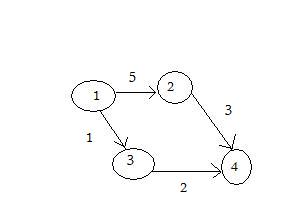
How to insert the values: at first input the number of vertices which is 4 for the above graph and 4 is the name of edges. Then, input the edge and the cost like 1 2 5, which means the cost from 1 to 2 is 5, then 1 3 1 which means the cost from 1 to 3 is 1 and so on. In the end, you will have to input the starting point, which could be 1 like in the above example.

Complexity:

The worst-case running time for the Dijkstra algorithm on a graph with n nodes and m edges is O(n^2) because it allows for directed cycles. It even finds the shortest paths from a source node to all other nodes in the graph. This is basically O(n^2) for node selection and O(m) for distance updates. While O(n^2) is the best possible complexity for dense graphs, the complexity can be improved significantly for sparse graphs.

Applications:

Telephone Network – In a telephone network the lines have bandwidth, BW. We want to route the phone call via the highest BW.
OSPF (open shortest path first) is a well known real-world implementation of Dijkstra’s algorithm used in internet routing.
A related problem is the traveling salesman problem, which is the problem of finding the shortest path that goes through every vertex exactly once, and returns to the start.

[catlist id=197].