Depth-first search (DFS) and breadth-first search (BFS) are two algorithms for traversing a graph. Graph traversal refers to the problem of visiting all the nodes in a graph in a particular manner. Each node may have to be visited more than once, and a root-like node that connects to all other nodes might not exist. Let us start first with DFS.
DFS
A Depth-first search (DFS) is a technique for traversing a finite undirected graph. DFS visits the child nodes before visiting the sibling nodes, that is, it traverses the depth of the tree before the breadth.
Example:
Legend: white means not visited, gray means in progress, black means finished processing the vertex:
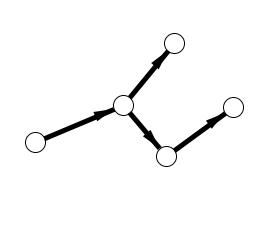
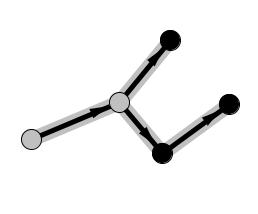
We begin with the node that has no predecessors and we mark it gray, because we can still go down:
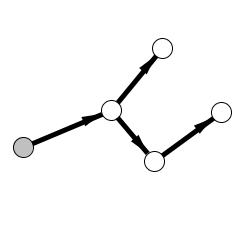
We move to the next option available:
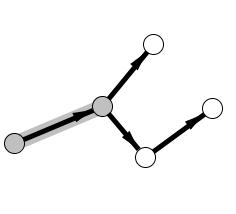
We can choose the path to follow, let’s go down:
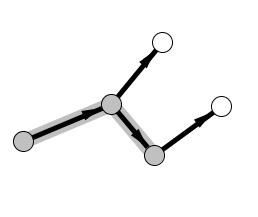
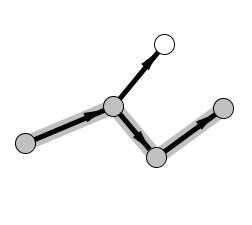
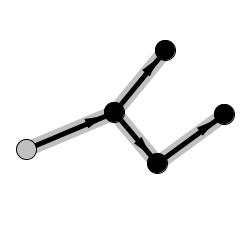
Now, we have nowhere to proceed, so we mark the node:
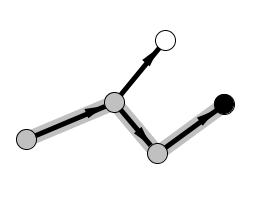
And then we go back to mark the visited nodes:
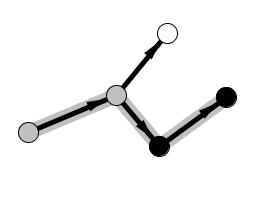
We encounter an unvisited node, so we proceed in that direction to visit it:
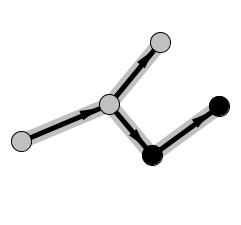
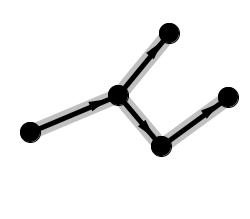
Again we have no place to continue, so we mark it and go back to mark the rest of the nodes:
Sample code:
#include< iostream >#include< conio.h >#include< stdlib.h >using namespace std;
int cost[10][10],i,j,k,n,stk[10],top,v,visit[10],visited[10];
int main()
{int m;
cout << "Enter the number of vertices = ";
cin >> n;
cout <<"Enter the number of edges = ";
cin >> m;
cout << "nEDGES n";
for(k=1;k< =m;k++)
{cin >>i>>j;
cost[i][j]=1;
}cout << "Enter starting vertex = ";
cin >>v;
cout << "ORDER OF VISITED VERTICES ";
cout << v <<" ";
visited[v]=1;
k=1;
while(k< n)
{for(j=n;j>=1;j--)
if(cost[v][j]!=0 && visited[j]!=1 && visit[j]!=1)
{visit[j]=1;
stk[top]=j;
top++;
}v=stk[--top];
cout<< v << " ";
k++;
visit[v]=0; visited[v]=1;
}return 0;
}
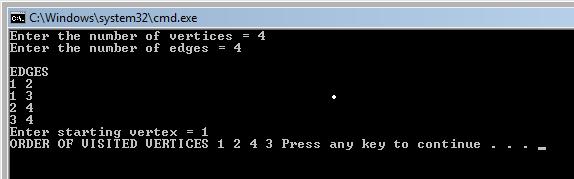
Output:
Code explanation:
Having the following graph:
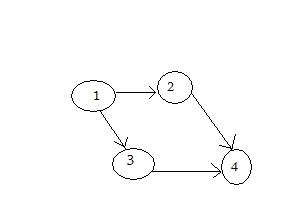
The number of vertices is 4, and the number of edges 4. When inserting the edges, for example we have a edge from 1 to 2, from 1 to 3, from 2 to 4 and for 3 to 4, and if we select the vertex 1 as the starting point, we will get the output from above. The algorithm runs just like in the example from above, it marks the visited vertices, and continues until there is no more vertices to visit.
Complexity:
Worst case performance : O( | V | + | E | ) for explicit graphs traversed without repetition, O(b^d) for implicit graphs with branching factor b searched to depth d
Worst case space complexity : O( | V | ) if entire graph is traversed without repetition, O (longest path length searched) for implicit graphs without elimination of duplicate nodes
[catlist id=197].
