Heapsort is a comparison based algorithm. It bases on building a heap tree from the data set, and then it removes the greatest element from the tree and adds it to the end of the sorted list. There are two ways to do this, either to add the highest value to the root of the tree, or as one of the left/right child with the greatest depth.
How it works:
The heap tree is built according to the data set. Then the greatest value is move to the root of the tree, and then it is removed. This represents the highest value from the data set, so it is added to the end of the sorted list. Next, the heap is reconstructed, and the second highest value is added to the top and then it is removed. This continues until the tree is empty and the list is full.
Step by step example :
Having the following list, let’s try to use heapsort to arrange the numbers from lowest to greatest:
Unsorted list: 15, 19, 10, 7, 17, 6.
Building the heap tree:
Start with the rightmost node at height 1 – the node at position 3 = Size/2. It has one greater child and has to be percolated down:
And it will look like this:
Then, we check the children of 19, but both are smaller so no swap is needed:
The children of 15 are 19 and 16, and is smaller, so a swap is required:
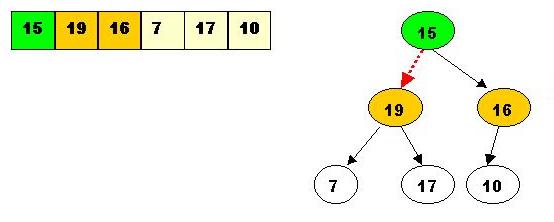
Also, 15 is smaller than 17 one of the children, so it is again time to swap :
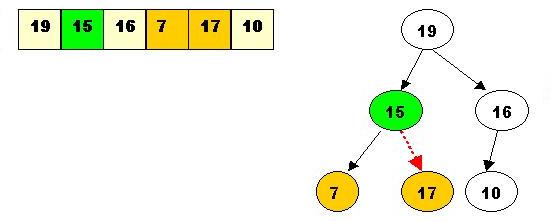
Now the heap was built.
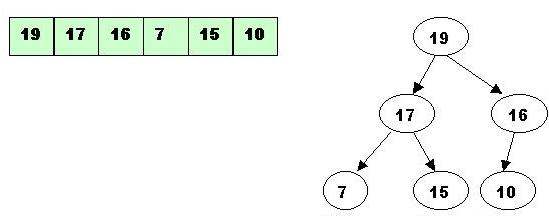
Next, it is time to sort the heap:
19, being the highest value, was removed from the top:
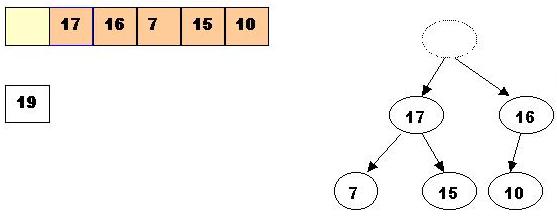
Swap 19 with the last element of the heap (As 10 will be adjusted in the heap, its cell will no longer be a part of the heap. Instead it becomes a cell from the sorted array ):

The element 10 will have to go down in the tree:
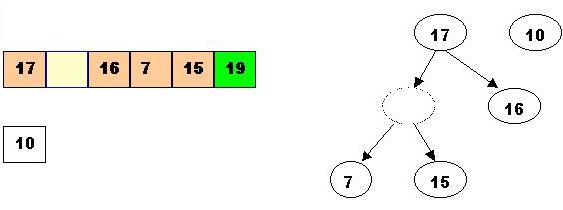
And again down one more level, 10 is less that 15, so it cannot be inserted in the previous hole :
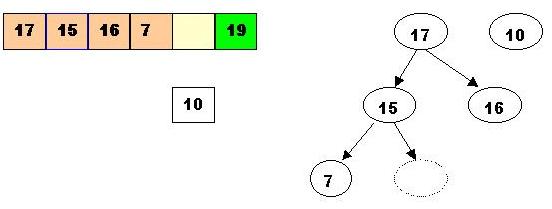
Now 10 has found the right spot:
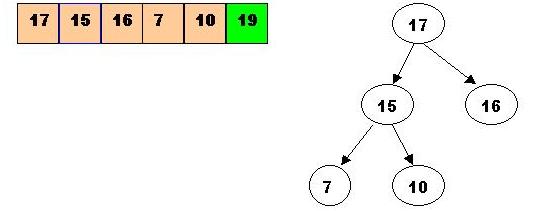
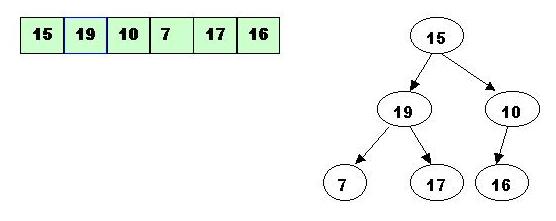
The next greatest element is 17, which has to be removed :
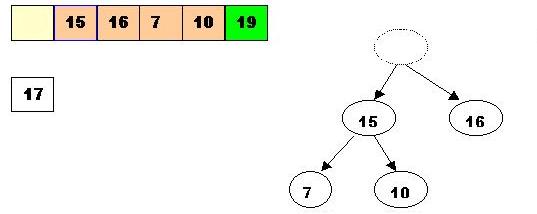
Also, swap 17 with the last element of the heap. As 10 will be adjusted in the heap, its cell will no longer be a part of the heap, instead it becomes a cell from the sorted array:
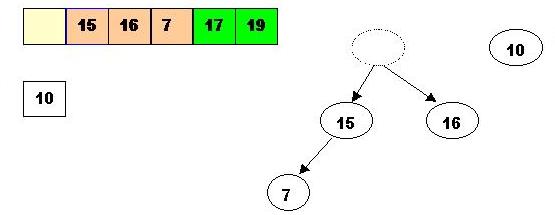
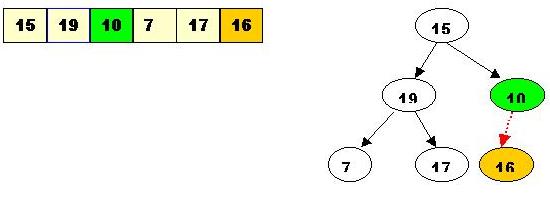
The element 10 is less than the children of the hole, and we percolate the hole down:
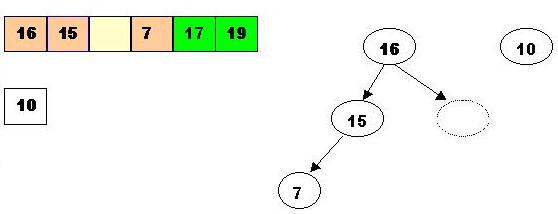
Insert 10 in the hole
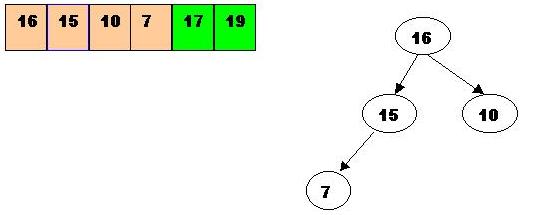
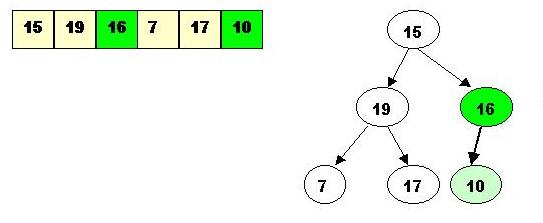
Delete the next biggest element which is 16:

Swap 16 with the last element of the heap. As 7 will be adjusted in the heap, its cell will no longer be a part of the heap, instead it becomes a cell from the sorted array:
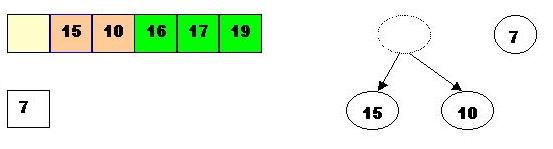
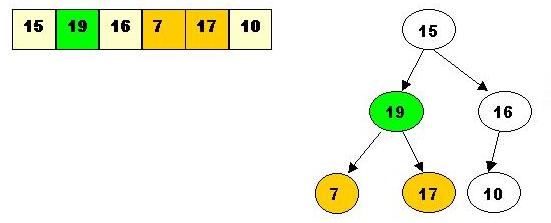
Go down one level to find the right position for 7:
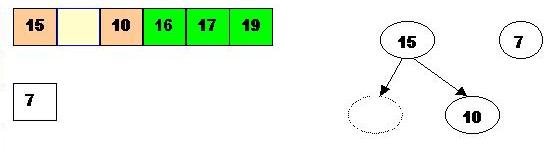
Remove 15:

Swap 15 with the last element of the heap. As 10 will be adjusted in the heap, its cell will no longer be a part of the heap, instead it becomes a position from the sorted array:
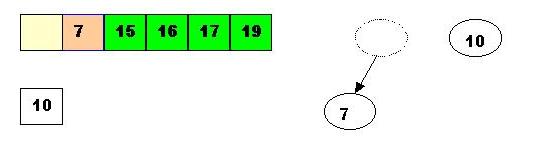
Store 10 in the hole (10 is greater than the children of the hole)

Remove 10:

Swap 10 with the last element of the heap. As 7 will be adjusted in the heap, its cell will no longer be a part of the heap, instead it becomes a cell from the sorted array:

Store 7 in the hole (as the only remaining element in the heap):

7 is the last element from the heap, so now the array is sorted :

Sample code:
#include< iostream >using namespace std;
void insert (int v[],int &N, int a)
{v[N]=a;
N++;
int child=N-1;
int parent=abs((child-1)/2);
while(parent >=0 )
{if(v[child]>v[parent])
{v[child]=v[parent]+v[child];
v[parent]=v[child]-v[parent];
v[child]=v[child]-v[parent];
child=parent;
parent=abs((child-1)/2);
}elseparent=-1;
}}int remove(int v[],int N)
{int a=v[0];
v[0]=v[N-1];
N--;
int parent=0;
int child=1;
while(child<=N-1)
{if(child+1< =N-1 && (v[child+1]>v[child]))
child++;
if (v[parent]< v[child])
{int aux=v[parent];
v[parent]=v[child];
v[child]=aux;
parent=child;
child=2*parent+1;}
elsebreak;
}return a;
}void heap_sort(int a[],int N,int v[])
{for(int i=N-1;i>=0;i--)
{N=i+1;
a[i]=remove(v,N);
}}void heap_gen1(int a[],int v[],int n)
{int N=1;
v[0]=a[0];
for(int i=1;i< n;i++)
{insert(v,N,a[i]);
}}void display(int a[],int n)
{for(int i=0;i < n;i++)
{cout << a[i] << " ";
}}int main()
{int *a=new int[100];
int *v=new int[100];
int n;
cout << "Please insert the number of elements to be sorted: ";
cin >> n; // The total number of elements
for(int i=0;i < n;i++)
{cout << "Input " << i << " element: ";
cin >> a[i]; // Adding the elements to the array
}cout << "Unsorted list:" << endl; // Displaying the unsorted array
for(int i=0;i < n;i++)
{cout << a[i] << " ";
}heap_gen1(a,v,n);
cout << "nGenerated Heap:n";
display(v,n);
cout << "nAfter sorting";
heap_sort(a,n,v);
cout << "n";
display(a,n);
return 0;
}
Output:

Code explanation:
The function heap_sort is the one that is removing the top of the heap tree and making the sorting list. The implementation of the algorithm simply follows the same steps as those from the above example.
Complexity:
HeapSort’s space-complexity is O(1), just a few scalar variables. It uses a data structure known as a max-heap which is a complete binary tree where the element at any node is the maximum of itself and all its children. A tree can be stored either with pointers as per the pictorial representation we are normally used to visualize, or by mapping it to a vector. Here if a node in the tree is mapped to the ith element of an array, then its left child is at 2i, its right child is at (2i+1) and its parent is at floor(i/2). We can construct a heap by starting with a an existing heap, adding an element at the bottom of the heap, and allow it to migrate up the father chain till it finds its proper position. Complexity T(n) = O(n*log (n)).
Advantages:
- it does not use recursion;
- works just as fast or any data order.
- there is no worst case scenario.
Disadvantages:
- slower that quick and merge sort;
- memory requirement, it requires both an array and a heap of size n;
- not stable.
Conclusion:
HeapSort is a good sorting algorithm, with a good complexity O(n*log(n)) for worst/base/average scenario. Heapsort is an in-place algorithm, but is not a stable sort.
[catlist id=197].
